Mastering Metrics: Six Sigma’s Dance with Powerful Regression Analysis

Six Sigma, initially developed by Motorola in the 1980s, is a set of techniques and tools aimed at improving processes by identifying and removing the causes of defects and minimizing variability. At its core, Six Sigma is data-driven, leveraging statistical methods to achieve a near-perfect level of quality, targeting a mere 3.4 defects per million opportunities.

The methodology is often associated with the DMAIC framework—Define, Measure, Analyse, Improve, and Control—which serves as a systematic approach to process enhancement. The goal? To elevate process performance, reduce variation, and sustain improvements.

Regression Analysis: A Six Sigma Ally

In the vast toolkit of Six Sigma, regression analysis stands out as a potent analytical method. Simply put, regression analysis is a statistical technique used to identify and quantify the relationship between variables. For Six Sigma practitioners, it’s an essential tool, especially during the “Analyse” phase of the DMAIC cycle.

Regression analysis can serve multiple purposes in a Six Sigma project:

• Determining the strength and nature of the relationship between an input (or independent variable) and an output (or dependent variable).
• Predicting the impact on the output if changes are made to the input.
• Verifying if a particular factor is a significant driver of a process outcome.

In Six Sigma environments, regression analysis aids practitioners in making data-driven decisions, uncovering hidden relationships, and validating or refuting hypotheses about process behaviour. By embedding this technique into Six Sigma projects, businesses can pave the way for more informed interventions and, ultimately, superior results.

The Confluence of Six Sigma and Regression Analysis

When “six sigma” and “regression analysis” come together, they form a robust alliance. With the disciplined approach of Six Sigma and the predictive insights offered by regression analysis, organisations can enhance their decision-making capabilities, optimise processes, and achieve a higher level of operational excellence.

This guide aims to explore this synergy further, diving deep into the nuances of regression analysis within the framework of Six Sigma. Whether you’re a seasoned Six Sigma Black Belt or someone just dipping their toes into the world of quality improvement, this guide will provide valuable insights into leveraging regression analysis effectively.

In This Guide

Basics of Regression Analysis:

What is Regression Analysis?

Regression analysis, in its simplest form, is a statistical method used to understand the relationship between dependent and independent variables. It primarily aims to model and analyse the relationships between variables, enabling predictions based on the observed data.

For instance, in a manufacturing setup, one might use regression analysis to determine how different factors such as machine speed or raw material quality (independent variables) affect the final product’s quality (dependent variable).

Purpose and Application

The primary purposes of regression analysis in the context of Six Sigma include:

• Predictive Analysis: Understanding how a change in the independent variable(s) might affect the dependent variable.
• Hypothesis Testing: Validating if a particular factor truly impacts the process outcome or if the observed relationship is merely by chance.
• Optimisation: Finding the best levels of input variables to achieve a desired output.

For Six Sigma practitioners, these purposes align seamlessly with the goals of process improvement and variability reduction.

Linear vs. Multiple Regression

While there are various types of regression analyses, the two most common types encountered in Six Sigma projects are:

• Linear Regression: It examines the relationship between one independent variable and one dependent variable, resulting in a linear equation that can be depicted on a two-dimensional graph. It’s the go-to method when you want to see how a single factor impacts the outcome.
• Multiple Regression: It involves multiple independent variables influencing a single dependent variable. This method is particularly useful in real-world scenarios where processes are often affected by various factors simultaneously.

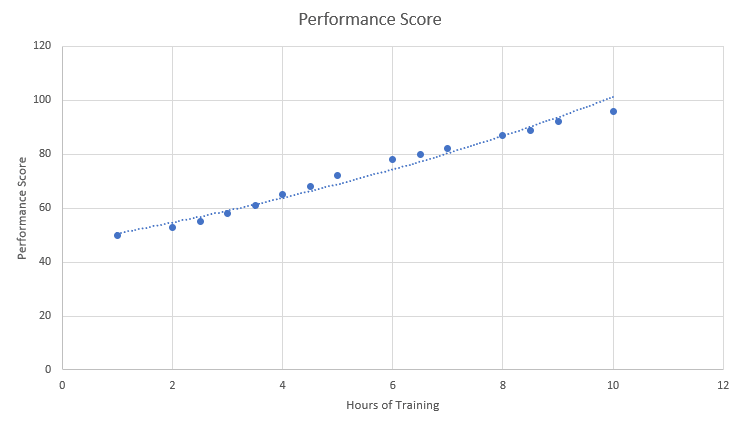
For example, if a company wants to study how both training hours and experience level (independent variables) affect an employee’s performance (dependent variable), they’d opt for multiple regression.

Conclusion of Basics

The power of regression analysis lies in its ability to model relationships, making it invaluable for Six Sigma projects. When utilised correctly, it offers clear insights into how different factors impact processes, enabling informed decision-making and strategic interventions.

Trending

Six Sigma Certification: What You Need To Know

Six Sigma DMAIC and Regression Analysis:

Setting the Stage: Define and Measure

At the outset of a Six Sigma project, practitioners embark on the Define phase, where they outline the scope of the project, set objectives, and identify stakeholders. This initial step sets the direction and prepares the team for the subsequent stages.

Following the define phase, the Measure phase kicks in. Here, professionals gather relevant data, ensuring it’s accurate and representative of the process in focus. This data serves as the foundation upon which regression analysis—and indeed the entire Six Sigma project—rests. It’s crucial, therefore, to invest time and resources into quality data collection.

The Heart of the Matter: Analyse

The Analyse phase is where regression analysis shines. Armed with data from the Measure phase, Six Sigma practitioners can:

• Identify Relationships: Through regression, we can discern if there’s a statistically significant relationship between variables. For instance, does the temperature of a machine (independent variable) influence the quality of the product (dependent variable)?
• Predict Outcomes: Regression analysis helps in predicting how changes in the independent variable(s) might influence the dependent variable. If we adjust the machine’s temperature, how will the product quality vary?
• Validate Hypotheses: A crucial aspect of the Analyse phase is hypothesis testing. Practitioners often have assumptions or theories about process behaviour. Regression allows them to validate or refute these hypotheses using collected data.

Acting on Insights: Improve

Once the relationships are identified and understood, the Improve phase begins. Here, teams design interventions based on insights from regression analysis. If, for example, regression reveals that machine temperature significantly impacts product quality, practitioners might optimise the temperature to achieve desired results.

Sustaining Excellence: Control

Post-implementation of improvements, the Control phase ensures that the changes hold, and the process remains within desired specifications. It’s here that regression analysis can again prove beneficial. By periodically running regression tests, practitioners can monitor if the established relationships between variables still hold or if new factors have emerged that might influence the process.

In Summary

Regression analysis, when embedded within the DMAIC framework of Six Sigma, empowers teams to make data-driven decisions, uncover hidden relationships, and implement sustainable improvements. From understanding process intricacies in the Analyse phase to monitoring long-term sustainability in the Control phase, the synergy between “six sigma” and “regression analysis” facilitates profound insights and actionable strategies.

Trending

Unleash the Power of Voice of the Customer Analysis: Empower Your Business Now

Types of Regression Analysis Used in Six Sigma:

Linear Regression: Simplifying Relationships

When we talk about regression, the most fundamental type that comes to mind is Linear Regression. This method is used when there’s a suspected linear relationship between an independent variable and a dependent variable.

In the context of Six Sigma, linear regression might be used to understand how a single factor, such as the pressure in a machine, impacts an outcome like product strength. The resulting model would provide a straight-line graph (or linear equation) that describes this relationship.

Multiple Regression: Unravelling Complexity

Processes are rarely influenced by just one factor. Often, there are multiple variables at play. Multiple Regression caters to such scenarios by allowing for multiple independent variables.

Imagine a production process where both the quality of raw material and the speed of the assembly line might affect the final product’s quality. Using multiple regression, Six Sigma practitioners can model and understand how these independent variables together influence the dependent variable.

Non-linear Regression: Beyond Straight Lines

Not all relationships can be described with a straight line. Sometimes, variables interact in ways that produce curves or other non-linear patterns. Non-linear Regression is the go-to method for these situations.

For example, in a chemical reaction process, the rate of reaction might initially increase with temperature but then level off or even decrease after reaching an optimal point. This relationship would be best modelled with non-linear regression.

Logistic Regression: Binary Outcomes

While most regression types predict continuous outcomes, there are scenarios in Six Sigma where the outcome is binary, such as pass/fail or defective/non-defective. In these cases, Logistic Regression is employed.

Consider a quality check process in manufacturing. If the aim is to predict whether a product will pass or fail based on various parameters, logistic regression would be the preferred technique.

Choosing the Right Tool for the Job

For Six Sigma practitioners, the choice of regression type hinges on the nature of the data and the specific relationships they seek to understand. It’s crucial to understand the nuances of each regression type to select the most appropriate method. In the dance between “six sigma” and “regression analysis,” the latter offers a suite of tools, each tailored for different scenarios and insights.

Challenges and Best Practices in Regression Analysis for Six Sigma:

Common Challenges with Regression Analysis:

Multicollinearity:

This refers to a situation where two or more independent variables in a regression model are highly correlated. It can distort the results and make it difficult to ascertain the individual effect of each variable.

For example, in a manufacturing setting, the temperature and humidity inside a facility might both influence product quality, but they could also be related to each other. If they rise and fall together, it’s challenging to determine their separate impacts.

Overfitting and Underfitting:

An overfitted model is one that’s too closely tailored to the existing data, capturing even its noise and anomalies. Such models might perform exceptionally well on the current data but fail to predict future outcomes accurately.

On the other hand, an underfitted model is too generalised and might not capture the nuances of the data, leading to inaccurate predictions.

Missing or Skewed Data:

Regression analysis relies on the quality and completeness of data. Missing data points or data that’s not representative of the actual process can lead to misleading results.

Incorrect Model Selection:

Choosing an inappropriate type of regression for the situation can lead to erroneous insights. For instance, using linear regression when the actual relationship is nonlinear might give an incomplete picture.

Best Practices with Regression Analysis:

Check for Multicollinearity:

Before finalising a regression model, especially in multiple regressions, it’s wise to check for multicollinearity. Techniques like the Variance Inflation Factor (VIF) can help identify if this issue exists.

Use Cross-Validation:

To avoid overfitting, one can split the dataset into training and test sets. The model is trained on one subset and tested on the other to ensure it generalises well to new data.

Data Integrity:

Always ensure that the data being used for regression is complete, accurate, and representative of the process. Regular audits and quality checks can help maintain data integrity.

Expert Consultation:

When in doubt, consulting with a statistician or a seasoned Six Sigma Black Belt can guide the right model selection and provide insights into the nuances of the data.

Wrapping Up The Regression Analysis Challenges:

While regression analysis offers powerful insights, like all tools, it’s essential to be aware of its limitations. By understanding potential pitfalls and adopting best practices, Six Sigma practitioners can harness the full potential of “six sigma” and “regression analysis,” ensuring their projects are grounded in accurate and insightful data-driven decisions.

Trending

Six Sigma: Demystify Process Capability Now

Implementing Regression Analysis in Your Six Sigma Project: A Step-by-Step Guide

Define Your Objective

Before diving into the data, have a clear understanding of what you want to achieve with the regression analysis. Are you trying to identify the main factors influencing a process? Predict future outcomes? This clarity will guide the entire analysis.

Data Collection

Gather data that aligns with your objectives. Ensure it is:

• Relevant: The data should directly relate to the variables you suspect are influencing your process.
• Accurate: Ensure measurements are correct and consistent.
• Complete: Missing data can skew results.

Choose the Right Type of Regression Analysis

Based on the nature of your data and the relationships you suspect:

• Linear regression for one independent variable.
• Multiple regression for multiple independent variables.
• Non-linear regression for non-linear relationships.
• Logistic regression for binary outcomes.

Data Preprocessing

Before running the regression:

• Check for multicollinearity.
• Handle missing data either by imputation or removal.
• Normalise or standardise variables, especially if they’re on different scales.

Run the Regression

Using statistical software like Minitab, JMP, or even Excel, input your data and run the selected regression analysis.

Interpret the Results

Look at the:

• Coefficients: They indicate the strength and direction of the relationship.
• P-values: They help in determining the statistical significance of the variables.
• R-squared value: It gives an idea of how well the model explains the variation in the data.

Validate the Model

Use techniques like cross-validation or split the data into training and test sets to ensure the model is not overfitted and can predict new data accurately.

Implement Insights

Based on the regression results, identify areas of improvement in the process, make necessary changes, and monitor the results.

Continual Monitoring

Regression isn’t a one-off activity. Periodically revisit the model, especially if there are significant changes in the process or environment. This ensures that the model remains relevant and accurate.

In Summary:

Implementing regression analysis in a Six Sigma project might seem daunting at first, but with a systematic approach, it becomes a manageable and highly rewarding task. As always, the key lies in understanding the data, choosing the right tools, and continually refining your approach based on real-world results.

Trending

Designing an Effective Control Plan in Six Sigma

The Power of Regression Analysis in Six Sigma

The Six Sigma methodology, with its structured approach to process improvement, requires robust analytical tools to make data-driven decisions. Among these tools, regression analysis stands out as a beacon, illuminating the complex relationships within processes and systems.

Delving into Data: Understanding Regression Analysis Complexity

Regression allows Six Sigma practitioners to navigate the intricate web of variables. Whether deciphering a simple linear relationship or untangling a multifaceted interaction of numerous elements, regression provides the map. It’s not just about identifying which variables matter but understanding how they interact and influence outcomes.

Caution on the Road: Using Regression Analysis Wisely

However, wielding such a potent tool comes with responsibilities. Practitioners must be aware of potential pitfalls, ensuring data’s accuracy, representativeness, and relevance. It’s crucial to understand that regression models are only as good as the data they’re built on. Periodic refining based on real-world feedback ensures they remain relevant and actionable.

Regression Analysis: A Symphony of Data and Methodology

When Six Sigma principles merge with the insights from regression analysis, it’s akin to orchestrating a symphony from what was once just noise. Data becomes music, guiding organizations towards their goals of continuous improvement and operational excellence.

In this age of data abundance, the harmonisation of “six sigma” and “regression analysis” provides a clear path, guiding businesses and professionals to unparalleled heights of efficiency and innovation.